课改十年话“计算”论文
课改十年话“计算”
■ 段娟
众所周知,在小学阶段学好计算并形成一定的运算能力,是令人终生受益的。许多年来,中国的基础教育一直引以为豪的就是“计算教学”,中国儿童的运算能力也一直在全球领先。
上世纪,我国的小学数学教育非常重视计算能力的培养,包括重视理解算理、掌握算法、形成技能、训练技巧,运用计算解答应用题,培养分析问题和解决问题的能力。自从2002 年我区进入省级课改实验,到今年正好十年,我们在调研中发现了计算教学值得深思的现象:以往对学生计算能力的要求,如计算方法、技巧与速度等,现在很少提了;学生的计算能力普遍下降了,主要表现在计算正确率下降,口算速度减慢等等;而学生对计算的兴趣并没有因此而提高,学生数学思维能力也没有得到应有的培养。到底是什么原因导致了这样的结果?我们经过课堂教学调查研究,发现了目前计算教学的几个误区。
1.过分依赖情境。有的教师片面认为,计算教学离不开情境,缺少了情境,似乎激发不起学生的学习兴趣。因此,有的课堂上情境设置是牵强附会的,有的纯粹是为了引出算式,经过一番不着边际的“看图说话”,等到从情境引出算式,已经花去了10 多分钟时间,影响了教学的进程。
2.算法多样化成了“终极目标”。有的教师对算法只求量上的“多”,学生展示同一思维层面的算法,教师一概叫好,而不管思维层面即质上的提升。一旦少了某种方法,教师就要千方百计地“牵引”。有的学生为了迎合教师的意图,想一些低价值、原始的方法来充数。这样一来,往往讨论一道题目就要花费10~15 分钟。而且算法“多”了以后,没有适时优化。在计算时,只要求学生用自己喜欢的方法计算,有的甚至于不要求学生掌握基本的计算方法。
3.课堂练习时间少。有的教师很少安排学生的课堂练习,片面认为现在计算教学的要求降低了,学生做习题就有机械、重复训练之嫌,翻来覆去“多样化”,挤占了练习时间,影响了学生基本计算技能的形成。
《标准2011 版》重新把“运算能力”列为核心概念,赋予运算能力一些新的内涵。《数学课程标准(2011 版)解读》中明确指出:“运算能力并非一种单一的、孤立的数学能力,而是运算技能与逻辑思维等的有机整合。在实施运算分析和解决问题的过程中,要力求做到善于分析运算条件,探究运算方向,选择运算方法,设计运算程序,使运算符合算理,合理简洁。换言之,运算能力不仅是一种数学的操作能力,更是一种数学的思维能力。”因此在标准2011 版的指引下,我们广大数学教师,应全面理解“运算能力”,更好地落实计算教学。本文拟从以下几个方面谈谈我们在计算教学的实践中研究的一些对策。
一、从解决问题中“应运而生”———凸显计算的需求
传统的计算教学,教师非常重视对知识的铺垫,一般按照“复习铺垫———出示例题———示范讲解———强化训练”的步骤进行。其最大优点是以学生原有的认知结构为起点,注重技能的掌握与形成。其缺点是枯燥、人文性弱,以致于很多学生不了解为什么要计算,为什么一定要用固定的方法计算,对于计算没有好感。
因此,课标实验教材中每一个计算例题都以解决实际生活中的问题为出发点,引入计算的学习,赋予计算以实际意义。学习数学的目的在于解决问题,而运算是解决问题的工具。学生在遇到问题时,首先要想到用什么方法解决问题,选择什么算法来解决,然后再算出结果。
如人教版二年级下册“万以内的加法和减法(一)”,就是以两个班合乘一条船为情境,通过解决“二(1)班、二(2)班能坐下吗?二(3)班、二(4)班合乘能坐下吗”的问题,引入23+31、32+39 的计算教学,再从“(1)班、(2)这条船上还能上几人?”引出68-54 的计算教学。
教师在计算教学中一定要注意让学生经历搜集信息———整理信息———提出问题———选择数据列式计算———最后解答问题的过程,使学生切实体会到计算的需求是来源于生活,计算为生活服务,从而更好地激发学习计算的内驱力。
二、注重直观操作与指导———突出算理的理解
何为算理?顾名思义,算理就是计算过程中的道理,是指计算过程中思维方式,是解决为什么这样算的问题。如计算24+35 时,就是根据数的组成进行演算的:24 是2 个十和4 个一组成的,35 是由3 个十和5 个一组成的,所以先把4 个一与5 个一相加得9 个一,再把2 个十与3 个十相加得5 个十,最后把5 个十和9 个一合并得59,这就是算理。
当学生进行了一定量的练习以后,发现了计算的规律:个位数只能与个位数直接相加、十位数只能与十位数直接相加,也就是相同数位上的数才能直接相加,最后再把几个得数合并,这是学生感悟算理的过程;最后进行优化计算过程,为了便于计算一般写成竖式形式,在此基础上引导学生抽象概括出普遍适用的计算法则:把相同数位对齐列出竖式,再从个位加起,满十向前一位进一,这就是算法。
从上面的分析可以看出:算理是客观存在的规律,为计算提供了正确的思维方式,保证了计算的合理性和正确性是算法的理论依据。
低年级计算教学中常常要借助学具操作来帮助学生理解算理。
案例:一年级下册《两位数减一位数(退位减法)》
学生在引出36-8的算式后,教师让学生运用前面学习的不退位减法的基础,自主尝试计算。不一会儿,有学生露出了愁容。
师:你们遇到什么困难了?
生:6 减8 不够减……
师:是呀,个位6 减8 不够减,那怎么办呢?我们借助小棒来寻找方法吧!
(师带领学生先摆出36 根小棒,然后想办法拿走8 根,看看还剩多少根。学生动手操作,并与同位的同学说一说自己是怎么拿的。)
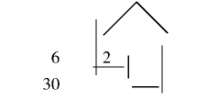
生1:我先拿走6 根,还差2 根,就从3 捆里面拆开1 捆,拿出2 根,这样就剩2捆零8根了。
师:你是把8 分成了6 和2,先减6,再从10里面减去2等于8,最后把20和8合起来是28。(板书:36- 8 =28)
 《课改十年话“计算”论文》
《课改十年话“计算”论文》
本文链接地址:http://www.oyaya.net/fanwen/view/103291.html
■ 段娟
众所周知,在小学阶段学好计算并形成一定的运算能力,是令人终生受益的。许多年来,中国的基础教育一直引以为豪的就是“计算教学”,中国儿童的运算能力也一直在全球领先。
上世纪,我国的小学数学教育非常重视计算能力的培养,包括重视理解算理、掌握算法、形成技能、训练技巧,运用计算解答应用题,培养分析问题和解决问题的能力。自从2002 年我区进入省级课改实验,到今年正好十年,我们在调研中发现了计算教学值得深思的现象:以往对学生计算能力的要求,如计算方法、技巧与速度等,现在很少提了;学生的计算能力普遍下降了,主要表现在计算正确率下降,口算速度减慢等等;而学生对计算的兴趣并没有因此而提高,学生数学思维能力也没有得到应有的培养。到底是什么原因导致了这样的结果?我们经过课堂教学调查研究,发现了目前计算教学的几个误区。
1.过分依赖情境。有的教师片面认为,计算教学离不开情境,缺少了情境,似乎激发不起学生的学习兴趣。因此,有的课堂上情境设置是牵强附会的,有的纯粹是为了引出算式,经过一番不着边际的“看图说话”,等到从情境引出算式,已经花去了10 多分钟时间,影响了教学的进程。
2.算法多样化成了“终极目标”。有的教师对算法只求量上的“多”,学生展示同一思维层面的算法,教师一概叫好,而不管思维层面即质上的提升。一旦少了某种方法,教师就要千方百计地“牵引”。有的学生为了迎合教师的意图,想一些低价值、原始的方法来充数。这样一来,往往讨论一道题目就要花费10~15 分钟。而且算法“多”了以后,没有适时优化。在计算时,只要求学生用自己喜欢的方法计算,有的甚至于不要求学生掌握基本的计算方法。
3.课堂练习时间少。有的教师很少安排学生的课堂练习,片面认为现在计算教学的要求降低了,学生做习题就有机械、重复训练之嫌,翻来覆去“多样化”,挤占了练习时间,影响了学生基本计算技能的形成。
《标准2011 版》重新把“运算能力”列为核心概念,赋予运算能力一些新的内涵。《数学课程标准(2011 版)解读》中明确指出:“运算能力并非一种单一的、孤立的数学能力,而是运算技能与逻辑思维等的有机整合。在实施运算分析和解决问题的过程中,要力求做到善于分析运算条件,探究运算方向,选择运算方法,设计运算程序,使运算符合算理,合理简洁。换言之,运算能力不仅是一种数学的操作能力,更是一种数学的思维能力。”因此在标准2011 版的指引下,我们广大数学教师,应全面理解“运算能力”,更好地落实计算教学。本文拟从以下几个方面谈谈我们在计算教学的实践中研究的一些对策。
一、从解决问题中“应运而生”———凸显计算的需求
传统的计算教学,教师非常重视对知识的铺垫,一般按照“复习铺垫———出示例题———示范讲解———强化训练”的步骤进行。其最大优点是以学生原有的认知结构为起点,注重技能的掌握与形成。其缺点是枯燥、人文性弱,以致于很多学生不了解为什么要计算,为什么一定要用固定的方法计算,对于计算没有好感。
因此,课标实验教材中每一个计算例题都以解决实际生活中的问题为出发点,引入计算的学习,赋予计算以实际意义。学习数学的目的在于解决问题,而运算是解决问题的工具。学生在遇到问题时,首先要想到用什么方法解决问题,选择什么算法来解决,然后再算出结果。
如人教版二年级下册“万以内的加法和减法(一)”,就是以两个班合乘一条船为情境,通过解决“二(1)班、二(2)班能坐下吗?二(3)班、二(4)班合乘能坐下吗”的问题,引入23+31、32+39 的计算教学,再从“(1)班、(2)这条船上还能上几人?”引出68-54 的计算教学。
教师在计算教学中一定要注意让学生经历搜集信息———整理信息———提出问题———选择数据列式计算———最后解答问题的过程,使学生切实体会到计算的需求是来源于生活,计算为生活服务,从而更好地激发学习计算的内驱力。
二、注重直观操作与指导———突出算理的理解
何为算理?顾名思义,算理就是计算过程中的道理,是指计算过程中思维方式,是解决为什么这样算的问题。如计算24+35 时,就是根据数的组成进行演算的:24 是2 个十和4 个一组成的,35 是由3 个十和5 个一组成的,所以先把4 个一与5 个一相加得9 个一,再把2 个十与3 个十相加得5 个十,最后把5 个十和9 个一合并得59,这就是算理。
当学生进行了一定量的练习以后,发现了计算的规律:个位数只能与个位数直接相加、十位数只能与十位数直接相加,也就是相同数位上的数才能直接相加,最后再把几个得数合并,这是学生感悟算理的过程;最后进行优化计算过程,为了便于计算一般写成竖式形式,在此基础上引导学生抽象概括出普遍适用的计算法则:把相同数位对齐列出竖式,再从个位加起,满十向前一位进一,这就是算法。
从上面的分析可以看出:算理是客观存在的规律,为计算提供了正确的思维方式,保证了计算的合理性和正确性是算法的理论依据。
低年级计算教学中常常要借助学具操作来帮助学生理解算理。
案例:一年级下册《两位数减一位数(退位减法)》
学生在引出36-8的算式后,教师让学生运用前面学习的不退位减法的基础,自主尝试计算。不一会儿,有学生露出了愁容。
师:你们遇到什么困难了?
生:6 减8 不够减……
师:是呀,个位6 减8 不够减,那怎么办呢?我们借助小棒来寻找方法吧!
(师带领学生先摆出36 根小棒,然后想办法拿走8 根,看看还剩多少根。学生动手操作,并与同位的同学说一说自己是怎么拿的。)
生1:我先拿走6 根,还差2 根,就从3 捆里面拆开1 捆,拿出2 根,这样就剩2捆零8根了。
师:你是把8 分成了6 和2,先减6,再从10里面减去2等于8,最后把20和8合起来是28。(板书:36- 8 =28)
 《课改十年话“计算”论文》
《课改十年话“计算”论文》

 ★读了本文的人也读了:
★读了本文的人也读了: