在“有理数”教学中训练学生思维能力的一些做法
着眼数学思考 暴露思维过程——在“有理数”教学中训练学生思维能力的一些做法
作者/周 强
摘 要:在数学教学中,培养能力的核心是发展学生思维能力。学生通过数学学习,需要得到思维的训练,学会数学思考。在教学中不仅要注重知识的积累,更要注重在教学过程中暴露思维过程,加强思维能力的训练,让学生在头脑中经历建立认知结构的过程,使学生的思维能力和品质得到提升,结合七年级“有理数”的教学内容和具体案例,探讨了在教学中进行思维训练的一些做法。
关键词:数学思维能力;数学思考;训练
训练学生思维能力,也是七年级学生面临的迫切需要。这个阶段的学生刚刚进入初中学习,思维还处于形象思维水平,还不习惯和适应初中学习的要求,因此,训练学生思维能力,促进他们的思维由形象思维发展成为经验型逻辑思维,对学生后续学习,以及身心发展有很大帮助。
一、利用概念、法则、性质的形成过程,训练学生的思维能力
在本章中,有不少概念、法则、性质。“任何一个概念、法则、性质都是客观事物的本质属性经过抽象和概括的结果。”在形成教学过程中,可以引导学生从实际生活或者数学经验两个方面出发,通过观察、比较、分析,通过数学思考,归纳出本质特征,并表述,从而形成概念法则和性质。
数学知识来源于生活,数学学习离不开生活。从实际问题抽象出数学概念和模型、构思证明方法等,是一种归纳方法和严密思考相结合,直观与抽象相结合的抓住事物本质进而构成系统的抽象过程,这是一种独特的数学思考方式。数学是培养学生思维能力,更重要的是培养这种思维方式,并将它用于实际生活。
具体教学实践中利用概念的实际生活背景,结合实际生活从中抽象出数学概念也符合学生的心理需求和认知规律,建立在学生的认知发展水平和已有的知识经验的基础之上的学习,能使学生的学习有意义和富有效率。
案例1:负数的引入
数的产生是实际生活的需要,负数这个概念同样来源于实际生活。其产生过程还蕴含着符号化的思想,因而,教学中可以进行如下设计:
活动:(1)请学生数老师手上拿着的粉笔。(若干支)(2)请一个学生数数他的同桌手中拿着的粉笔。(没有笔)(3)老师手中的粉笔折断为两半,请学生用一个数表示半根粉笔。(4)一学生阅读:零上5℃,零下11℃,零上11℃等,由同桌用数来表示。表示出:-5、+11、-11等,让学生感受引入符号的必要性。
通过活动说明数的产生和发展离不开生活和生产的需要。向学生渗透数学来源于实践的观点,同时进行对数学从实际生活中抽象、归纳、符号化的思维训练。
案例2:有理数的加法
活动一:约定进球为正,输球为负,进球和输球的和为净胜球,红队胜蓝队3比1,蓝队胜黄队2比0,黄队平红队1比1。解决如下问题:(1)红队进球数为多少?(+3)+(+1)=4。(2)红队失球数为多少?(-1)+(-1)=-2。(3)红队净胜球为多少?4+(-2)=2。依次解决蓝队、黄队如上问题,得到9个有理数加法的算式。
活动二:观察以上算式,归纳有理数加法运算的法则。观察过程中教师提示学生观察加数的类比、加数的符号和绝对值分别与和的符号和绝对值的关系,进而归纳出运算法则。
以上活动一中,从实际生活中得到一系列算式,反应了数学来源于实际生活,通过活动二进行数学思考,要求学生通过观察、比较、加以归纳、抽象、概括得到数学法则,正是体现数学思考的良好素材,通过暴露思维的过程,既揭示了数学知识的本源,又对学生的思维能力进行了训练。同时归纳过程中体现的分类思想,符号化思想,也是数学思维训练的目标。这类活动对于学生提升思维品质有极大帮助。
本章中,某些概念法则和性质有类似之处。我们还可以在它们的形成教学过程中,让学生将已经熟知知识“类似的”建立在新的知识基础上,形成新的知识。这里就可以训练学生类比联想、类比推理的能力。
案例3:有理数加法的结合律
教师通过一系列问题引导学生思考:(1)学习了有理数加法 的交换律后,启发学生比较现在所学的交换律和小学里的交换律有何不同?可以发现适合的范围有扩充。(2)小学所学的加法的结合律适合于有理数范围吗?提醒学生意识到加法的交换律和结合律都是加法的运算性质,可以大胆猜想。(3)你能举例试试吗?于是,引导学生在有理数范围内试验加法结合律的适用与否,从而直接类似地“搬来了”加法的结合律。
这个过程中利用性质之间的关联,引导学生主动建构知识,不但能培育学生良好的学习习惯,而且通过学生类比思考,合情猜想,周密验证,从而得到结论的思维过程,能很好地训练学生类比、观察、猜想的思维能力。
二、利用概念、法则和性质的运用过程,训练学生的思维能力
在本章中,概念、法则和性质的运用与数学运算有着紧密联系。数学运算的实质是根据数学运算的定义以及运算法则和性质,从已知数据推导出结果的过程。这一过程中包含有判断、演绎推理等过程。在应用过程中暴露思维过程,也能达到训练学生分析与综合的思维能力的目的。
案例4:有理数加法法则的运用训练
训练中要求学生结合有理数的加法法则,在运算过程中放慢步伐,展示判断运算种类,根据法则确定和的符号和绝对值的过程。于是将加法运算训练题分解成多步填空题,设计如下表格供训练:
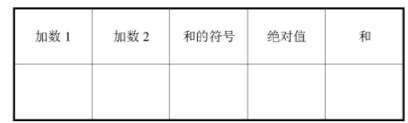
学生在填空的过程中需对照所给问题,结合法则完成判断、运用、推导的过程。既加深对法则的理解,又在运用的过程中得到逻辑推理能力的训练。
需要指出的是:新课程改革之后,不少教师在实践过程中忽略甚至放弃运算过程中的思维训练,其实是不可取的。计算过程中的思维过程同样是数学思考,遵从法则运算不仅能训练学生推理的能力,更对学生形成良好的世界观和价值观大有裨益。
在课堂教学中训练学生思维能力是多方面的,以上只是结合“有理数”这章的知识内容特点分析了一些做法。在实践中着眼数学思考,展示思维过程,着力于训练学生思维能力,学生的思维能力和品质就能得到良好发展,同时对于学生形成良好的学习品质和健全发展也有深刻的影响。
参考文献:
刘兼,孙晓天。《义务教育数学课程标准》解读。北京师范大学出版社,2002-05.
(作者单位 湖北省麻城市宋埠中心学校) 《在“有理数”教学中训练学生思维能力的一些做法》
本文链接地址:http://www.oyaya.net/fanwen/view/105059.html
作者/周 强
摘 要:在数学教学中,培养能力的核心是发展学生思维能力。学生通过数学学习,需要得到思维的训练,学会数学思考。在教学中不仅要注重知识的积累,更要注重在教学过程中暴露思维过程,加强思维能力的训练,让学生在头脑中经历建立认知结构的过程,使学生的思维能力和品质得到提升,结合七年级“有理数”的教学内容和具体案例,探讨了在教学中进行思维训练的一些做法。
关键词:数学思维能力;数学思考;训练
训练学生思维能力,也是七年级学生面临的迫切需要。这个阶段的学生刚刚进入初中学习,思维还处于形象思维水平,还不习惯和适应初中学习的要求,因此,训练学生思维能力,促进他们的思维由形象思维发展成为经验型逻辑思维,对学生后续学习,以及身心发展有很大帮助。
一、利用概念、法则、性质的形成过程,训练学生的思维能力
在本章中,有不少概念、法则、性质。“任何一个概念、法则、性质都是客观事物的本质属性经过抽象和概括的结果。”在形成教学过程中,可以引导学生从实际生活或者数学经验两个方面出发,通过观察、比较、分析,通过数学思考,归纳出本质特征,并表述,从而形成概念法则和性质。
数学知识来源于生活,数学学习离不开生活。从实际问题抽象出数学概念和模型、构思证明方法等,是一种归纳方法和严密思考相结合,直观与抽象相结合的抓住事物本质进而构成系统的抽象过程,这是一种独特的数学思考方式。数学是培养学生思维能力,更重要的是培养这种思维方式,并将它用于实际生活。
具体教学实践中利用概念的实际生活背景,结合实际生活从中抽象出数学概念也符合学生的心理需求和认知规律,建立在学生的认知发展水平和已有的知识经验的基础之上的学习,能使学生的学习有意义和富有效率。
案例1:负数的引入
数的产生是实际生活的需要,负数这个概念同样来源于实际生活。其产生过程还蕴含着符号化的思想,因而,教学中可以进行如下设计:
活动:(1)请学生数老师手上拿着的粉笔。(若干支)(2)请一个学生数数他的同桌手中拿着的粉笔。(没有笔)(3)老师手中的粉笔折断为两半,请学生用一个数表示半根粉笔。(4)一学生阅读:零上5℃,零下11℃,零上11℃等,由同桌用数来表示。表示出:-5、+11、-11等,让学生感受引入符号的必要性。
通过活动说明数的产生和发展离不开生活和生产的需要。向学生渗透数学来源于实践的观点,同时进行对数学从实际生活中抽象、归纳、符号化的思维训练。
案例2:有理数的加法
活动一:约定进球为正,输球为负,进球和输球的和为净胜球,红队胜蓝队3比1,蓝队胜黄队2比0,黄队平红队1比1。解决如下问题:(1)红队进球数为多少?(+3)+(+1)=4。(2)红队失球数为多少?(-1)+(-1)=-2。(3)红队净胜球为多少?4+(-2)=2。依次解决蓝队、黄队如上问题,得到9个有理数加法的算式。
活动二:观察以上算式,归纳有理数加法运算的法则。观察过程中教师提示学生观察加数的类比、加数的符号和绝对值分别与和的符号和绝对值的关系,进而归纳出运算法则。
以上活动一中,从实际生活中得到一系列算式,反应了数学来源于实际生活,通过活动二进行数学思考,要求学生通过观察、比较、加以归纳、抽象、概括得到数学法则,正是体现数学思考的良好素材,通过暴露思维的过程,既揭示了数学知识的本源,又对学生的思维能力进行了训练。同时归纳过程中体现的分类思想,符号化思想,也是数学思维训练的目标。这类活动对于学生提升思维品质有极大帮助。
本章中,某些概念法则和性质有类似之处。我们还可以在它们的形成教学过程中,让学生将已经熟知知识“类似的”建立在新的知识基础上,形成新的知识。这里就可以训练学生类比联想、类比推理的能力。
案例3:有理数加法的结合律
教师通过一系列问题引导学生思考:(1)学习了有理数加法 的交换律后,启发学生比较现在所学的交换律和小学里的交换律有何不同?可以发现适合的范围有扩充。(2)小学所学的加法的结合律适合于有理数范围吗?提醒学生意识到加法的交换律和结合律都是加法的运算性质,可以大胆猜想。(3)你能举例试试吗?于是,引导学生在有理数范围内试验加法结合律的适用与否,从而直接类似地“搬来了”加法的结合律。
这个过程中利用性质之间的关联,引导学生主动建构知识,不但能培育学生良好的学习习惯,而且通过学生类比思考,合情猜想,周密验证,从而得到结论的思维过程,能很好地训练学生类比、观察、猜想的思维能力。
二、利用概念、法则和性质的运用过程,训练学生的思维能力
在本章中,概念、法则和性质的运用与数学运算有着紧密联系。数学运算的实质是根据数学运算的定义以及运算法则和性质,从已知数据推导出结果的过程。这一过程中包含有判断、演绎推理等过程。在应用过程中暴露思维过程,也能达到训练学生分析与综合的思维能力的目的。
案例4:有理数加法法则的运用训练
训练中要求学生结合有理数的加法法则,在运算过程中放慢步伐,展示判断运算种类,根据法则确定和的符号和绝对值的过程。于是将加法运算训练题分解成多步填空题,设计如下表格供训练:

学生在填空的过程中需对照所给问题,结合法则完成判断、运用、推导的过程。既加深对法则的理解,又在运用的过程中得到逻辑推理能力的训练。
需要指出的是:新课程改革之后,不少教师在实践过程中忽略甚至放弃运算过程中的思维训练,其实是不可取的。计算过程中的思维过程同样是数学思考,遵从法则运算不仅能训练学生推理的能力,更对学生形成良好的世界观和价值观大有裨益。
在课堂教学中训练学生思维能力是多方面的,以上只是结合“有理数”这章的知识内容特点分析了一些做法。在实践中着眼数学思考,展示思维过程,着力于训练学生思维能力,学生的思维能力和品质就能得到良好发展,同时对于学生形成良好的学习品质和健全发展也有深刻的影响。
参考文献:
刘兼,孙晓天。《义务教育数学课程标准》解读。北京师范大学出版社,2002-05.
(作者单位 湖北省麻城市宋埠中心学校) 《在“有理数”教学中训练学生思维能力的一些做法》

 ★读了本文的人也读了:
★读了本文的人也读了: