“线性回归直线”的教学思考
“线性回归直线”的教学思考
重庆市复旦中学 袁 亮
一、问题的提出
在新课标教材《数学3(必修)》第二章统计第三小节变量间的相关关系课本中介绍了用每个样本点与线性回归直线对应点的纵坐标差的平方和最小来刻画“从整体上看,各点与直线的距离最小”,并用最小二乘法推导出线性回归方程的斜率与纵截距。
在刻画“从整体上看,各点与直线的距离最小”中新课标教材《数学3(必修)》给出了另外三种方式。但是在选择上没有给出任何关于哪样的程度是可靠性强及合理的解释,就直接选取了每个样本点与线性回归直线对应点的纵坐标差的平方和最小来刻画。
那么上述三种方式模拟出的直线是怎样的形式,以及怎样的程度才是比较合理的和可靠性强的?
二、讨论与分析
以新课标教材探究中人体脂肪含量和年龄关系为例
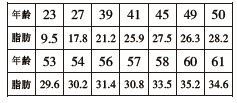
如果我们只用除去最后一个数据即点(61,34,6)来用最小二乘法拟合回归直线,则可计算得到回归方程为y=0.5775x-0.4854,如果代入61年龄检验可得到y=34.74,与样本中所采集的数据34.6之间的偏差为0.14。
2.1教材所提供的其他三种方式拟合回归直线。
2.1.1各点到直线距离和最小来拟合回归直线。
我们把“各点到直线距离和最小来拟合回归直线”记作方法一。
把我们所获得的组数据(最后一组数据用来检验回归直线的拟合情况用),记为:
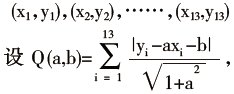
通过利用LINGO软件编程可以实现计算出Q(a,b)最小时的a,b,进而得到此法下拟合的回归直线方程为y=0.6x-2.2,如果代入最后一点的数据61检验可得到y=34.4,与样本中所采集的数据34.6之间的偏差为-0.2。
2.1.2直线两侧点个数基本相同来拟合回归直线。
我们把“直线两侧点个数基本相同来拟合回归直线”记作方法二。
可以想到如果把13这组数据描绘成散点图,然后用一条斜向下的直线去分割数量得到的直线肯定不合适;所以我们还是用和数据走势一致的直线去拟合回归直线,同时也很容易想到这样的直线不定。
通过散点图的观察和计算13组数据所构成点的坐标与原点的斜率可以看出斜率变化不大,因而我们用过原点的直线去拟合回归直线并让直线两侧的点数基本相同,根据斜率大小找到回归直线方程为y=0.5639x,如果代入最后一个点的数据61检验可得到y=34.3979,与样本中所采集的数据34.6之间的偏差为-0.2021。
2.1.3用多条直线的斜率、纵截距平均数来表示回归直线。
我们把“用多条直线的斜率、纵截距平均数来表示回归直线”记作方法三。
不难想到这多条直线的选取应该根据样本点的走势来看,同时可以想到这种方法去拟合的直线不定。
根据样本描绘的散点图选择了多组与整体走势相近的7组点得到直线的斜率和纵截距,然后用斜率、纵截距的平均值作为回归直线的斜率和纵截距,从而得到的拟合回归直线方程为y=0.639x-2.5534,如果代入最后一个点的数据61检验可得到y=36.43,与样本中所采集的数据34.6之间的偏差为1.827。
2.2比较上述的四种方法拟合的回归直线的特点。
首先说到方法一,这是最容易想到的,同时也是最让人接受的方法,在实际教学过程中很多学生都会问到这个方法为什么教材直接就否定了而采用“最小二乘法”,即利用各个样本点与回归直线偏差的平方和来拟合,且从图形中也可以看到,点到直线的距离与点到直线的偏差“等价”,两者之间差一个系数而已。
其实两个方法之间的确有差异,虽然看起两者只差一个系数,但是这个数却与回归直线的斜率有关,即在确定直线之前是一个变量。再有比较两种方法可以看到利用“最小二乘法”得到的估计值比较接近实际测量值。
其次说到方法二和方法三,在实际教学中学生很容易想到这两个方法使用起来一不方便,二这两个方法所确定的直线不唯一也就不好判定谁具有最佳的拟合程度。而且从刚才利用两个方法拟合到的直线也可以看出与实际测量值的差距比较大。
2.3最小二乘法的特点。
追溯最小二乘法的历史可以知道早在1806年法国科学家勒让德独立发现,并成功的让高斯通过统计40天的谷神星的观测数据计算得到了谷神星的轨迹。从这点来说最小二乘法不仅可以很好的拟合两个变量的直线形式,而且还可以拟合两个变量的曲线形式。
不过任何方法都有其缺点,利用最小二乘法拟合直线时对两个变量的数据要求比较高,要使得数据的随机误差满足正态分布,同时也可以验证当样本点中出现了异常点时,用最小二乘法拟合得到的直线则误差较大。
三、结束语
在比较了最小二乘法与其他的方法拟合回归直线的优缺点后,可以让学生更好的体会到最小二乘法的优越性和必要性,使得数学学习更加自然;而且回顾最小二乘法的历史也让学生体会数学的魅力。
再者在新课程的教学背景下,从教材的编排中可以看出,现在教学更需要注重知识的实用性和过程性,不仅要求学生要知道怎样去用,更要明白为什么可以这么用。
【参考文献】
[1]人民教育出版社中学数学室。普通高中新课程实验教课书。数学3必修(A版)[M].北京:人民教育出版社,2005
[2]冯守平。全最小一乘法[J].安徽。安徽大学学报。2009
[3]马小平。回归直线的拟合效果探究[J].山东。中学数学杂志。

 ★读了本文的人也读了:
★读了本文的人也读了: