勾股定理的逆定理应用探究

勾股定理的逆定理应用探究
　　
　　江苏　新沂　●刘　莉
　　
　　《义务教育数学课程标准（2011年版）》（以下简称《课标》）在课程“目标与内容”七学段～九学段中指出：“探索勾股定理及其逆定理，并能运用它们解决一些简单的实际问题。”勾股定理及其逆定理是初中数学中非常重要的定理，华罗庚把它称为“茫茫宇宙星际交流的语言”，西方一些国家把它称为“毕达哥拉斯定理”。勾股定理及其逆定理揭示了直角三角形三边的数量关系，体现了“数形统一”的数学思想。勾股定理和它的逆定理不但是解直角三角形的重要依据，而且是各省市中考必考的知识点，同时在实际生活中的应用也十分广泛。这里我们不探索勾股定理的应用，只探索勾股定理的逆定理的应用。笔者在长期的初中数学教学中发现，有许多学生在涉及到判断三角形的形状、计算图形的面积时，还是不知道应该如何利用勾股定理的逆定理来解决问题。由于勾股定理及其逆定理把直角三角形中有一个直角的“形”的特征，转化为三边之间的“数”的关系，也就是把几何学与代数学有机地结合在一起了。因此，我们应用勾股定理的逆定理抽象出数学方程模型或者进行图形的转化是判断三角形的形状、计算图形的面积问题的一种行之有效的方法。在应用勾股定理的逆定理解决问题的时候，一定要让学生去思考、讨论、交流甚至是探究，让他们经历解题的过程，最终树立“数形结合”的数学思想和方法，正如《课标》所说：“它不仅包括数学的结果，也包括数学结果的形成过程和蕴含的数学思想方法。”下面，笔者就勾股定理的逆定理的应用谈谈自己的看法。
　　
　　一、利用勾股定理的逆定理判断三角形的形状
　　
　　例1：已知在三角形中，a、b、c分别是它的三边，并且a+b=10，ab=18，c=8，判断三角形的形状。
　　
　　分析：由于题目中涉及两边之和与两边的积，所以先结合完全平方公式得出a2+b2的值，再检验a2+b2与c2的大小，就可以得出相应的结论。
　　
　　所以，凡是给出三角形的三边或者边之间的关系判断三角形的形状，都应考虑应用勾股定理的逆定理来进行判断。
　　
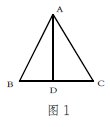
　　变式训练：如图l所示，已知：在△ABC中，AB=13，BC=l0，BC边上的中线AD=12。求证：△ABC是等腰三角形。
　　
　　二、利用勾股定理的逆定理与勾股定理结合计算图形的面积
　　
　　例2：如图2所示，已知在四边形ABCD中，∠ABC=90°，AB=3，BC=4，AD=12,CD=13。求四边形ABCD的面积。
　　
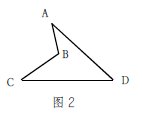
　　分析：由于这是不规则的四边形，所以不能直接计算面积，可根据题目所给数据特征，联想勾股数，先连接AC，转化成两个三角形的面积之差，并判断两个三角形的形状，就可以实现四边形向三角形转化，得出相应的结论。所以，计算不规则的四边形的面积，一般要通过构造直角三角形再利用三角形的面积的和或差进行计算。
　　
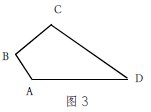
　　变式训练：如图3所示，已知四边形ABCD中，∠B=90°，AB=3，BC=4，CD=12，AD=13，求四边形ABCD的面积。
　　
　　以上我们讨论了利用勾股定理的逆定理判断三角形的形状以及利用勾股定理的逆定理与勾股定理结合的方式计算图形的面积的问题，利用这种方法应该说是一种比较简捷、有效的方法。我们在引导学生利用勾股定理的逆定理解决实际问题时，一定要让学生进行变式训练，并进行一题多解、一题多练，从而达到举一反三、触类旁通的目的。同时，我们还要注意发挥学生的主体作用，让学生主动地去发现问题、探究问题进而解决问题，从而培养学生的思维能力和创新能力。《课标》指出：“教师要处理好讲授与学生自主学习的关系，引导学生独立思考、主动探索、合作交流，使学生理解和掌握基本的数学知识与技能，体会和运用数学思想与方法，获得基本的数学活动经验。”让学生掌握基本的数学知识和基本的数学技能不是最根本的目的，最根本的目的是通过数学学习，训练学生的思维能力，提高他们的创新性和创造性。
　　
　　在学习和应用勾股定理的逆定理过程中，我们可以结合“综合与实践”课给学生灌输“生活数学”的思想。《课标》指出：“‘综合与实践’内容设置的目的在于培养学生综合运用有关的知识与方法解决实际问题，培养学生的问题意识、应用意识和创新意识，积累学生的活动经验，提高学生解决现实问题的能力。”我们要遵循《课标》的要求和教学理念，灵活地应用勾股定理的逆定理，把勾股定理的逆定理的应用同实际生活紧密地联系在一起。我们要让学生明白：数学知识来源于生活，但又要应用于生活。没有生活就没有数学知识，数学知识如果不应用于生活，也就失去了数学知识的价值。
　　
　　总之，勾股定理的逆定理的应用是十分广泛的。我们在引导学生应用勾股定理的逆定理时，一定要注意方式、方法，让学生灵活地掌握和应用。