用几何画板验证全等三角形”
用几何画板验证全等三角形”
东台市实验中学教育集团 崔恒刘
《几何画板》是美国Key Curriculum Press 公司制作的优秀教育软件,它可以给我们创造一个实际“操作”数学、做数学“实验”的环境,如任意拖动某点、线,观察图形的变化,猜测、验证结论,在观察、探索、发现的过程中增加对各种图形的感性认识,形成丰厚的几何经验背景,从而更有助于我们对数学的学习和理解。下面我带领同学们用几何画板实验验证:为什么三角形全等的条件只有SSS、SAS、ASA这3个基本事实和AAS这1个推论呢?SSA为什么不可以呢?用SSS、SAS、ASA、AAS判定两个三角形全等,其本质是给定的条件能不能唯一确定三角形,现在我们以边为线索,先从三边开始探究:
一、 三边对应相等
已知△ABC的三边AB=c,BC=a,CA=b,求作△ABC。
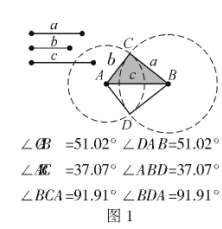
过程:先作线段AB=c,然后分别以A、B为圆心,b、a为半径画圆,如果两圆不能相交,则说明给定的三边不能组成三角形,这验证“三角形的两边之和大于第三边,两边之差小于第三边”。如图1,我们看到,两圆相交于两点C、D,连接AC、AD、BC、BD,则得到△ABC和△ABD,度量三对角,发现它们分别相等,则说明这两个三角形全等。从这里可以看出,有了三边的长度,不用考虑角的大小,就能把三角形唯一确定下来。这说明若三角形的三边相等,则两三角形全等。
本文链接地址:http://www.oyaya.net/fanwen/view/223452.html
东台市实验中学教育集团 崔恒刘
《几何画板》是美国Key Curriculum Press 公司制作的优秀教育软件,它可以给我们创造一个实际“操作”数学、做数学“实验”的环境,如任意拖动某点、线,观察图形的变化,猜测、验证结论,在观察、探索、发现的过程中增加对各种图形的感性认识,形成丰厚的几何经验背景,从而更有助于我们对数学的学习和理解。下面我带领同学们用几何画板实验验证:为什么三角形全等的条件只有SSS、SAS、ASA这3个基本事实和AAS这1个推论呢?SSA为什么不可以呢?用SSS、SAS、ASA、AAS判定两个三角形全等,其本质是给定的条件能不能唯一确定三角形,现在我们以边为线索,先从三边开始探究:
一、 三边对应相等
已知△ABC的三边AB=c,BC=a,CA=b,求作△ABC。
过程:先作线段AB=c,然后分别以A、B为圆心,b、a为半径画圆,如果两圆不能相交,则说明给定的三边不能组成三角形,这验证“三角形的两边之和大于第三边,两边之差小于第三边”。如图1,我们看到,两圆相交于两点C、D,连接AC、AD、BC、BD,则得到△ABC和△ABD,度量三对角,发现它们分别相等,则说明这两个三角形全等。从这里可以看出,有了三边的长度,不用考虑角的大小,就能把三角形唯一确定下来。这说明若三角形的三边相等,则两三角形全等。
二、两边对应相等
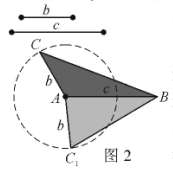
①无角相等:已知△ABC的两边AB=c,CA=b,求作△ABC。
过程:先作线段AB=c,再以A点为圆心,b为半径画圆,在圆上任取一点C与A、B连接,所形成的三角形均满足两边AB=c,CA=b的条件,如图2,拖动点C,可以看到,这样的三角形有无数,这说明两边对应相等的两个三角形不全等。
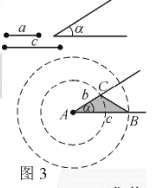
②两边的夹角相等:已知△ABC的两边AB=c,AC=b和它们的夹角∠BAC=∠α,求作△ABC。
过程:先作∠BAC=∠α,然后以点A为圆心,分别以c,b为半径画圆,交∠A的两边于B、C两点,连BC,则图3中有一个确定的△ABC,满足条件AB=c,AC=b,∠BAC=∠α。这说明若三角形的两边及两边的夹角对应相等,则两三角形全等。
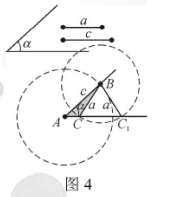
③一边的对角相等:已知△ABC的两边AB=c,BC=a和边BC的对角∠BAC=∠α,求作△ABC。
过程:先作∠BAC=∠α,然后以点A为圆心,以c为半径画圆,交∠A的一边于B点,再以B点为圆心,a为半径画圆,可以看到,这个圆与∠BAC的另一边有两个交点,如图4(也可能是一个交点,也可能没有交点),即满足条件的三角形不能唯一确定,这说明若三角形的两边及一边的对角对应相等,则两三角形不一定全等。
由上面的三点讨论知:当已知三角形的两边对应相等时,必须再知道它们的夹角相等,才能确定这两个三角形全等,而SSA不能判定两个三角形全等。
三、有一边相等
类似地,我们用画板实验有一边相等的情形,这个留给同学们自己尝试

 ★读了本文的人也读了:
★读了本文的人也读了: