例说PISA数学样题特点

例说PISA数学样题特点
　　
　　扬州市梅岭中学　袁红艳
　　
　　PISA（Programme for International Student Assessment，国际学生评估项目的缩写）是一项由经济合作与发展组织（Organization for Economic Co-operation and Development，OECD）统筹的学生能力国际评估计划。主要对接近完成基础教育的15岁学生进行评估，测试学生能否掌握参与社会所需要的知识与技能。
　　
　　第一次PISA评估于2000年首次举办，此后每3年举行一次。评估主要分为3个领域：阅读素养、数学素养及科学素养。由这3项组成评估循环核心，在每一个评估周期里，有三分之二的时间会对其中一个领域进行深入评估，其他两项则进行综合评测。
　　
　　PISA会在各个国家中抽取4500名到1万名以初三与高一为主的15岁学生担任调查对象，以测试学生是否能够掌握社会所需的知识与技能，因此试题着重于应用及情境化。受测学生必须灵活运用学科知识与认知技能，针对情境化的问题自行建构答案，因此能深入检视学生的基础素养。PISA测试的重点是看学生全面参与社会的知识和技能，对学生阅读、数学和科学能力的考查并不限于书本知识，还包括成年人生活中需要的知识和技能。
　　
　　自国际学生评估项目（PISA）在评估中提出“素养”这个概念以来，PISA 一直以学生数学素养、阅读素养、科学素养为核心内容，考查青少年是否具备未来生活所需的知识与技能， 以及是否为终身学习奠定了良好的基础。数学素养（Matheracy）作为素养中的一个重要组成部分，其内涵具有一定的历史性。1986 年，美国数学教师协会（NCTM）拟定的学校数学课程改革将数学素养作为课程与教学的中心议题，将“懂得数学的价值、对自己的数学能力有信心、有解决数学课题的能力、学会数学交流、学会数学的思想方法”作为有数学素养的标志。
　　
　　PISA所有数学测试题的呈现方式是以一个主题为单元，文字描述实际背景，学生需要经历将实际问题“数学化”的过程；突出了数学试题的现实性，强化了对文字的理解，以及在真实的新情景下解决问题的能力。PISA数学样题有如下特点：
　　
　　一、以实际生活的情境为问题的主题
　　
　　由于PISA注重考查同学们运用数学知识解决实际问题的能力，所以其设置的数学问题一般都有一个实际生活的情境。它不同于同学们平时学习的课本中所设置的练习题，那些练习题设计的主要目的是用来帮助同学们巩固和掌握所学的数学知识，而PISA所设计的问题的主要目的在于考查同学们能否解决各种情境中的问题。
　　
　　例如“地衣”问题：
　　
　　全球性暖化会造成一部分冰川融化的结果。约在冰川消失的十二年后，微小的植物——地衣，会开始在岩石间生长。地衣生长的形式犹如圆圈一般，圆圈的直径与地衣年龄之间的关系约可用下列公式来表示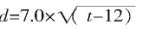：，t≥12,其中，d 表示圆圈直径（毫米），t 表示冰川消失后的年数。
　　
　　问题1：利用公式，算出冰川消失后16年的地衣直径。写出你的计算方法。
　　
　　问题2：安安测量出某地区地衣的直径为35毫米。请问在这地区的冰川是多少年前消失的？写出你的计算方法。（问题1参考答案：14毫米；问题2参考答案：37年。）
　　
　　【点评】它来自于同学们的实际生活情景，是同学们在实际生活中很可能会碰到的问题，必须运用数学知识才能解决。但其目的并不只是考查同学们已掌握多少解决该题需要用到的知识，而是考查同学们在这样一个实际情境中，如何分析问题、选择什么数学知识来解决这样一个实际问题。
　　
　　二、重视对图表类型问题的考查
　　
　　在PISA数学样题中，多有图表类型的问题，几乎每道题都有图表或表格。PISA要考查的是同学们运用数学解决现实生活中的问题，当同学们在阅读各种报刊、电视、互联网上的信息时，常常会看到各种形式的图表或表格，同学们要能够会分析、理解这些图表。
　　
　　例如“滑板”问题：
　　
　　奕涵是一位狂热的滑板迷。他到一家名为SKATERS的商店去确认几种价格。 在这家店你可以买到一个组装好的滑板。或者，你也可以买一块板子、4个为一组的轮子、2个为一组轮架和一套金属零件，来组装你自己专属的滑板。 商店里的产品价格如下表。
　　
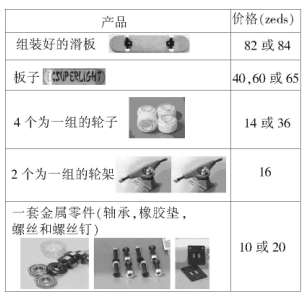
　　问题 1： 奕涵想组装他自己的滑板。在这家店自己组装滑板的最低价格及最高价格分别是多少？
　　
　　（a）最低价格： zeds
　　
　　（b）最高价格： zeds
　　
　　问题 2： 店里提供三种不同的板子、两组不同的轮子和两套不同的金属零件。但只有一组轮架可以选择。奕涵可以组装几种不同的滑板？
　　
　　A.6 B.8 C.10 D.12
　　
　　问题 3： 奕涵有120 zeds，他想用这些钱买最贵的滑板。奕涵在以下4个部件分别可以负担多少钱？在下表中写出你的答案。
　　
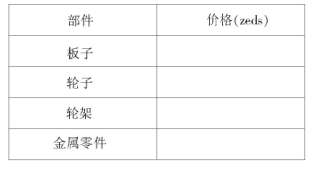
　　（参考答案：问题1答案：最低价为80zeds，最高价为137zeds；问题2答案：D；问题3答案：板子65，轮子14，轮架16，金属零件20.）
　　
　　【点评】问题1是封闭型问题，要求同学们正确阅读表格，理解日常语言和数学语言的关系，整合情境中的复杂信息，理解非连续文本的含义，理解组合的意义，并判断出最高和最低组合的形式。该问题没有具体的策略和方法，需要逐一尝试，可以考查出同学们不同的能力等级。问题2是选择题，要求同学们在约束条件下进行排列组合并论证，难度较小，并且由于是选择题也增加了随机猜测的可能性。问题3是开放题型，要求同学们在所有的组合中进行比较筛选，充分运用思考和推理，创造性地解答并进行反思。该问题要求同学们将现实问题“数学化”，并进行深刻的理解和反思，直至提炼出具有迁移性的问题和解决策略。
　　
　　三、重视对数学各门课程的综合考查
　　
　　由于PISA要求同学们解决的是实际生活中的问题，所以这些问题往往不会只涉及数学课程的某一点，而是会涉及数学多门课程的知识内容，如算术、代数和几何等。它要求同学们能够综合地运用自己所学的各门课程的知识来解决问题。
　　
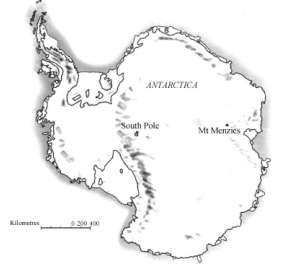
　　例如“大陆面积”问题：
　　
　　上图为南极洲地图，利用地图的比例尺，估算出南极洲的面积。写出你的作法并解释你是如何估计的。 （若利用作图能帮助你估计的话，可直接画在地图上。）
　　
　　（参考答案1：画一个正方形或长方形估计出面积在12 000 000平方公里和18 000 000平方公里之间；参考答案2：画一个圆形估计出面积在12 000 000平方公里和18 000 000平方公里之间；参考答案3：加上数个规则的几何图形估计面积在12 000 000平方公里和18 000 000平方公里之间；参考答案4：运用其他正确方法得出面积在12 000 000平方公里和18 000 000平方公里之间。）
　　
　　【点评】本题测试的问题涉及数学学科领域的各个问题单元，考查同学们的估算、建模、面积公式、运算多方面能力，考查同学们的思维过程，答案多样，方法思路正确给部分分，以给同学们更多的自由和空间。在出题方式上以实际生活的情境为问题的主题，重视对数学各门课程的综合考查，注重考查同学们解决生活问题的能力。
　　
　　通过上述PISA样题的展示我们不难发现：PISA是一种为终身学习能力的发展而建立的动态模式。在这种模式下，蕴含着这样一种表述：在这个迅速发展的瞬变时代，同学们不可能在学校里学到将来生活所需的一切知识和技能，必须在同学们具备阅读、数学、科学等方面的基础上，努力培养他们的自主学习能力；学校不仅要让同学们学会learn to know（学会事实），更要同学们学会how to learn（如何学习），让同学们能够对自己的学习过程、学习策略进行反思，并且可以在独立和集体的情境中进行学习。